++ 50 ++ 分数の約分 265928-分数の約分

数学 約分の話 証明編

 分数を習う中に約分も当然含まれていますが 同義ではないのになぜ必ず約分が前提なのか・ だとしたらその出典や学習要綱が存在するのか そこが気になっての質問でありました。小学5年生の算数 分数の約分・通分 練習問題プリント 小学5年生の算数分数の約分・通分練習プリントを無料ダウンロード・印刷できます。

分数の約分

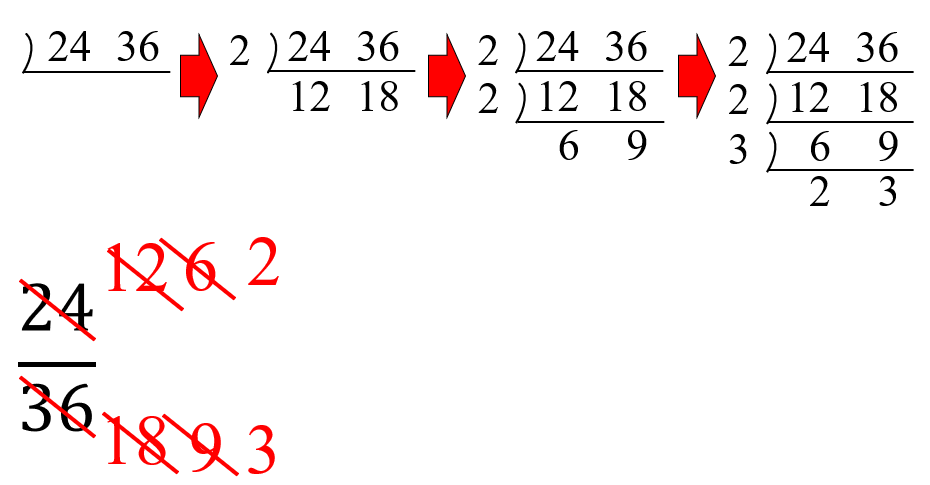
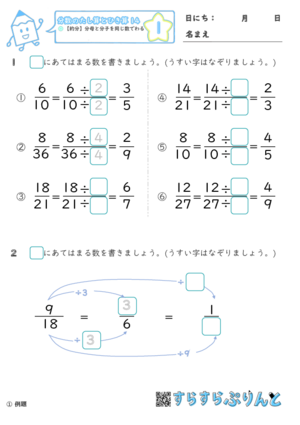
分数の約分-ツイート 無料ダウンロード・印刷できる小学5年生の算数プリント 分数の約分・通分を繰り返し練習できるプリントです。 分数の約分・通分（1） 答え 分数の約分・通分（2） 答え 分数の約分・この分数の性質を利用して、 分母・分子を同じ数で割って、分母と分子を最小の分数にすることを 約分 (やくぶん) と言います。 約分の方法 約分をおこなう方法としては、まず基本的な方法として分母・分子を同じ数で割っていき割り切れなくなるまで繰り返すという方法があります。

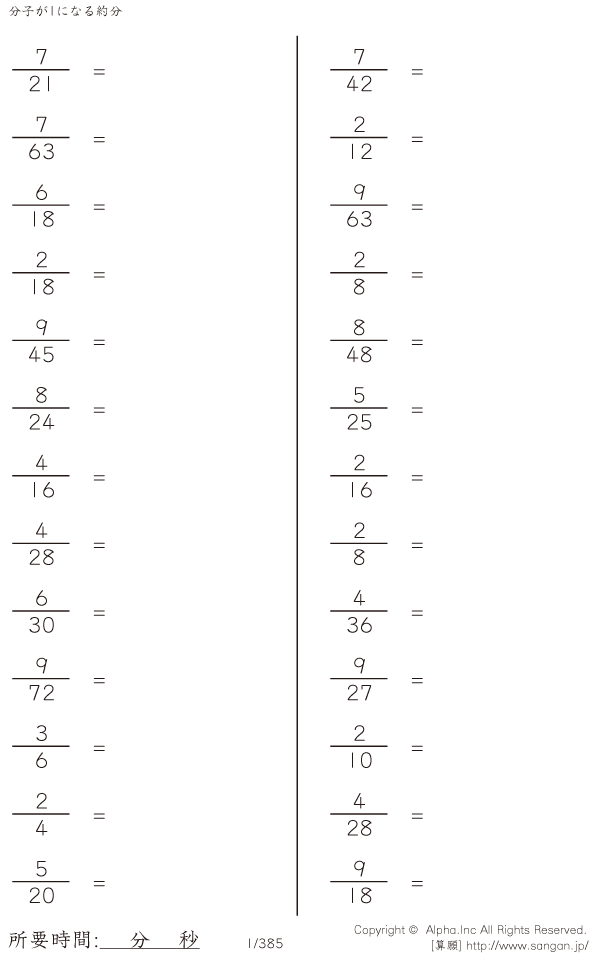
分子が1になる約分 問題 001 385

分数の割り算をするときのコツは、① 計算途中で約分できる場合は約分する ② 帯分数の割り算は仮分数に直してから計算する の2つがあります。それぞれ、詳しくい見ていきましょう。 約分とは、分数の「分母」と「分子」の2つの数の公約数で「分母」と「分子」を割ったものです。 実質的に、分母と分子の数の 最大公約数 で割って、それ以上約分ができない分数を求められることが多くなっています。 小学校5年生の後半で 約数 倍数を習った後に 分数の約分 通分を習います。ここで「分数きらーい 分数にがーて」になる人が たくさん登場します。 分数は 計算をすすめる前の 割り算です。 分数は 今まで勉強してきた数とは 異なる性質を持ちます。

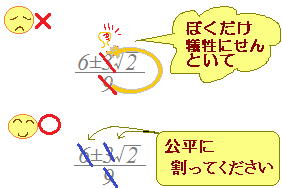
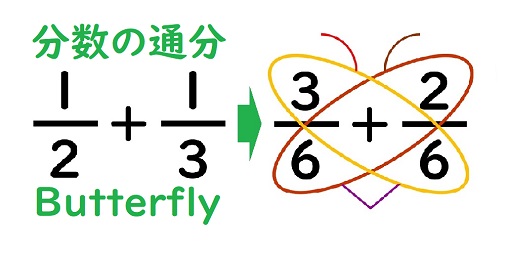
分数の足し算・引き算の手順 通分する（分母を揃える） 分子同士を計算する なぜ通分しなければいけないのか？ たとえば分母が等しい時を考えてみると、計算は普通の足し算・引き算と同じ要領でスムーズにできるのがわかります。 分母が同じという分数分の分数のやり方 まとめ 分数の中に分数！ こんな形が出てきたときには 上÷下 つまり、分子÷分母の計算を解いていけば 答えを出すことができます！ 見た目は難しそうに見えますが 単純な割り算を計算するだけですからね約分は、分数を簡単にするのに使用します。 また、2つの分数の分母を同じにして約分することを通分といいます。 分数の足し算や引き算は通分してから計算し、最後に約分をして答えを計算します。 約分した分数のことは、既約分数といいます。 関連計算機

分数の約分のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

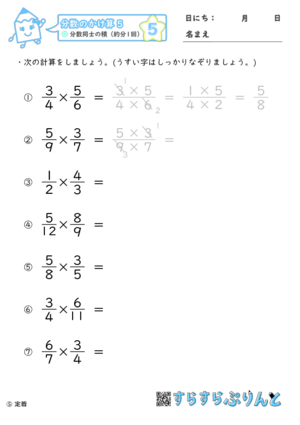分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	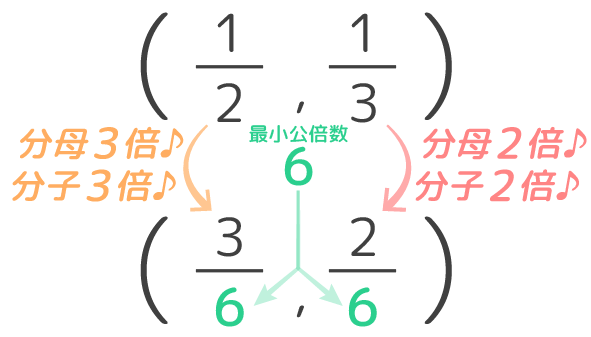分数足し算約分なし 問題 031 100
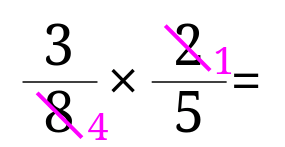分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	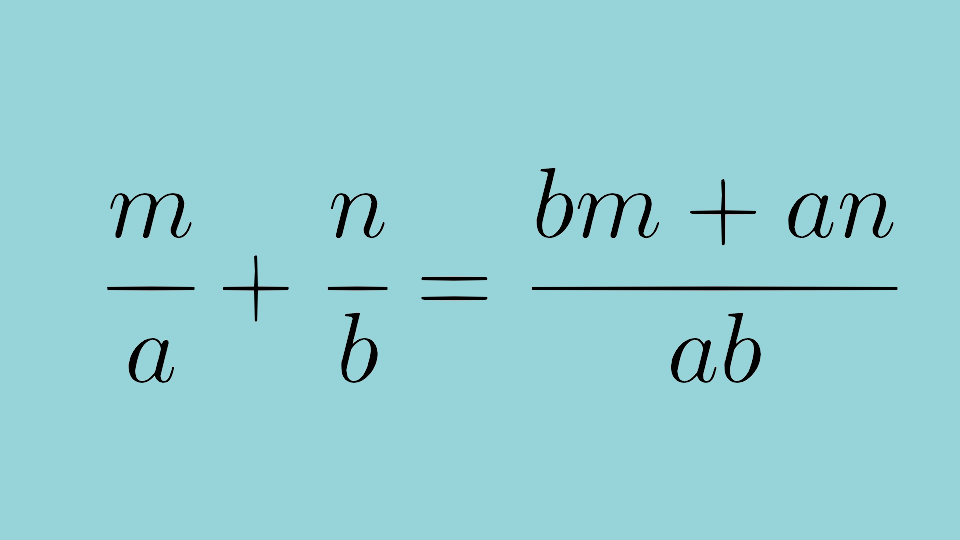分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	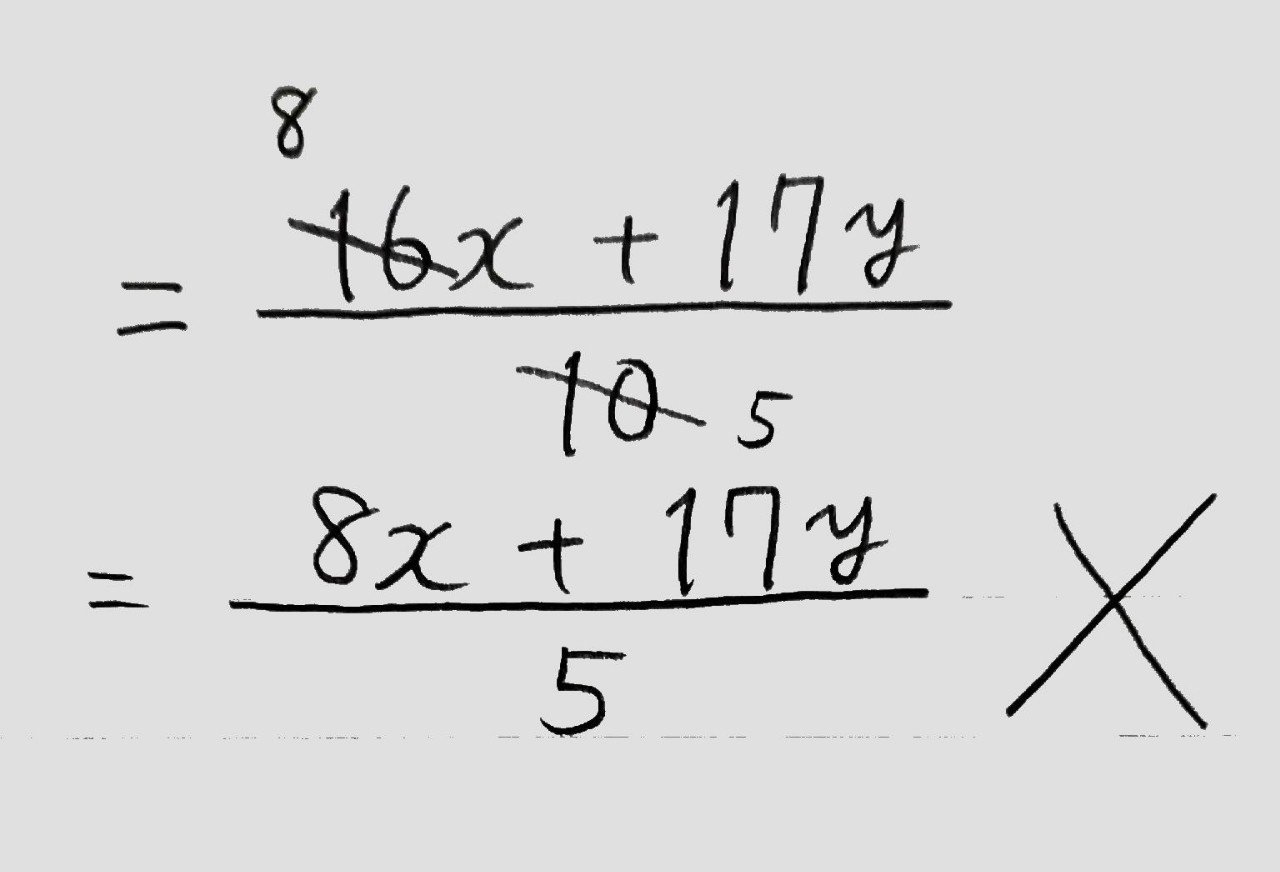分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	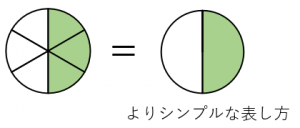分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	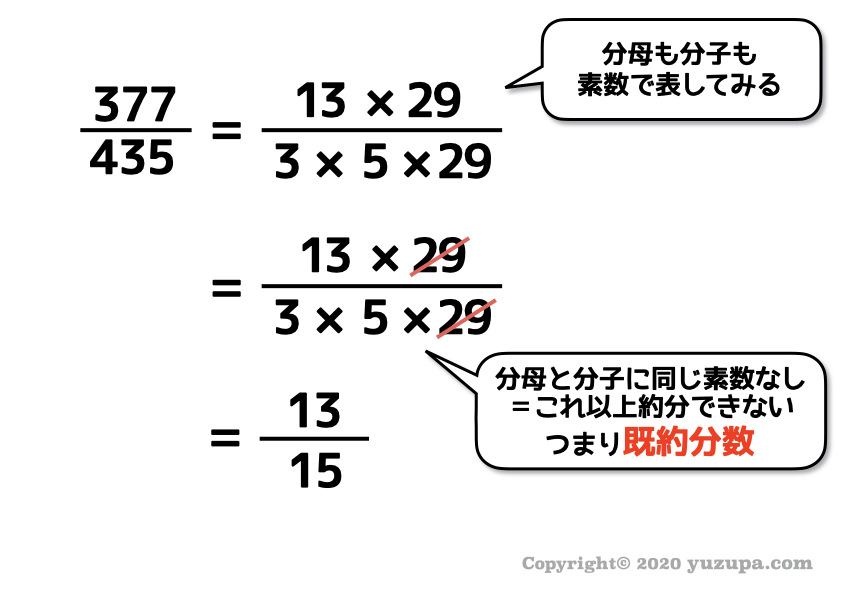分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	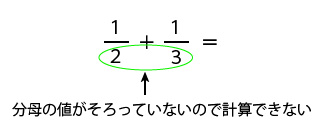分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	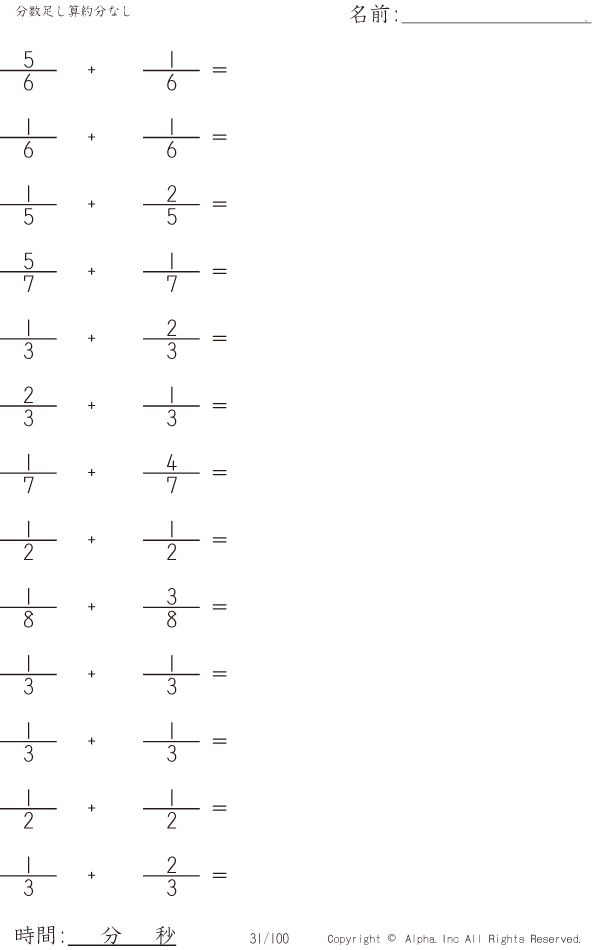分数足し算約分なし 問題 031 100	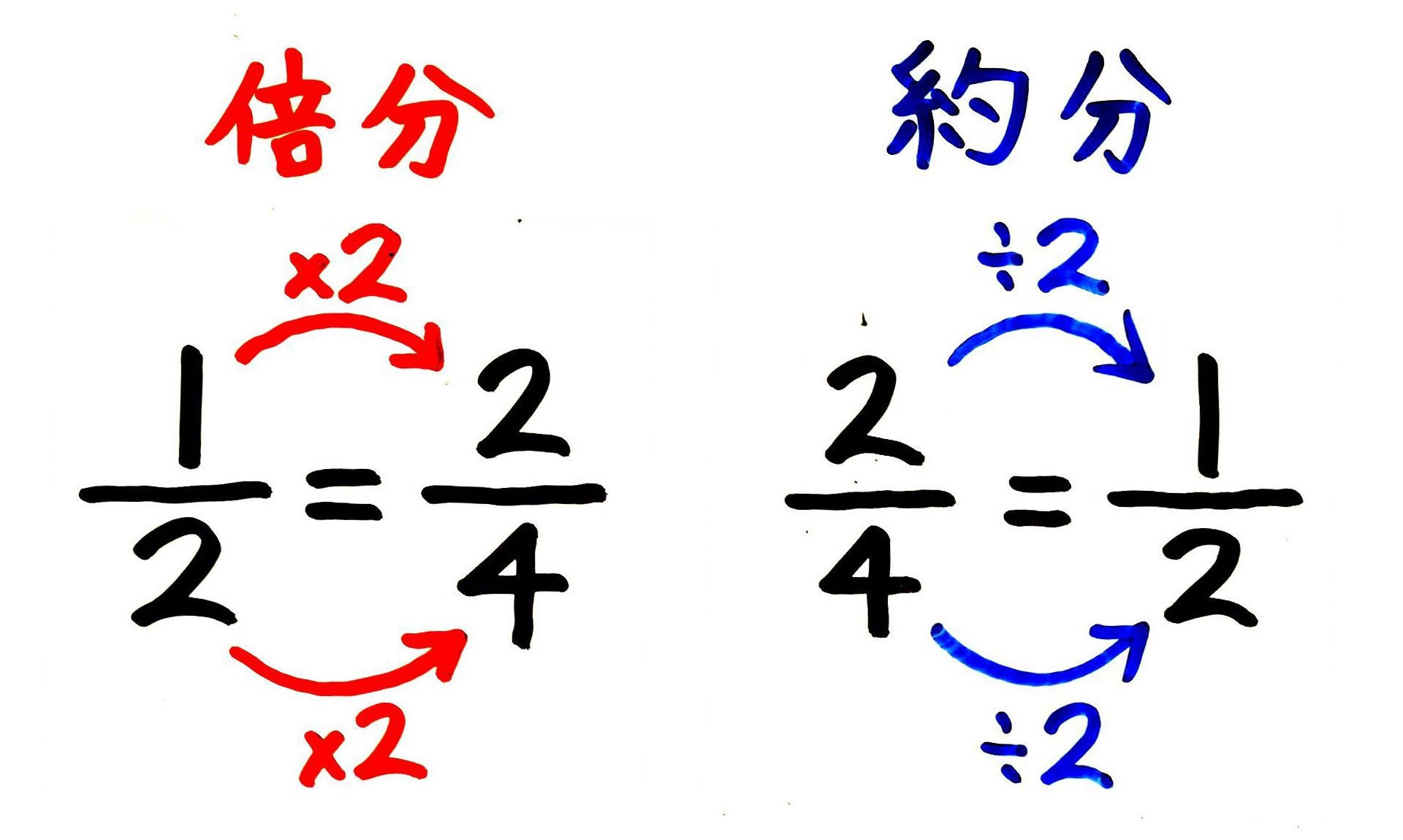分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	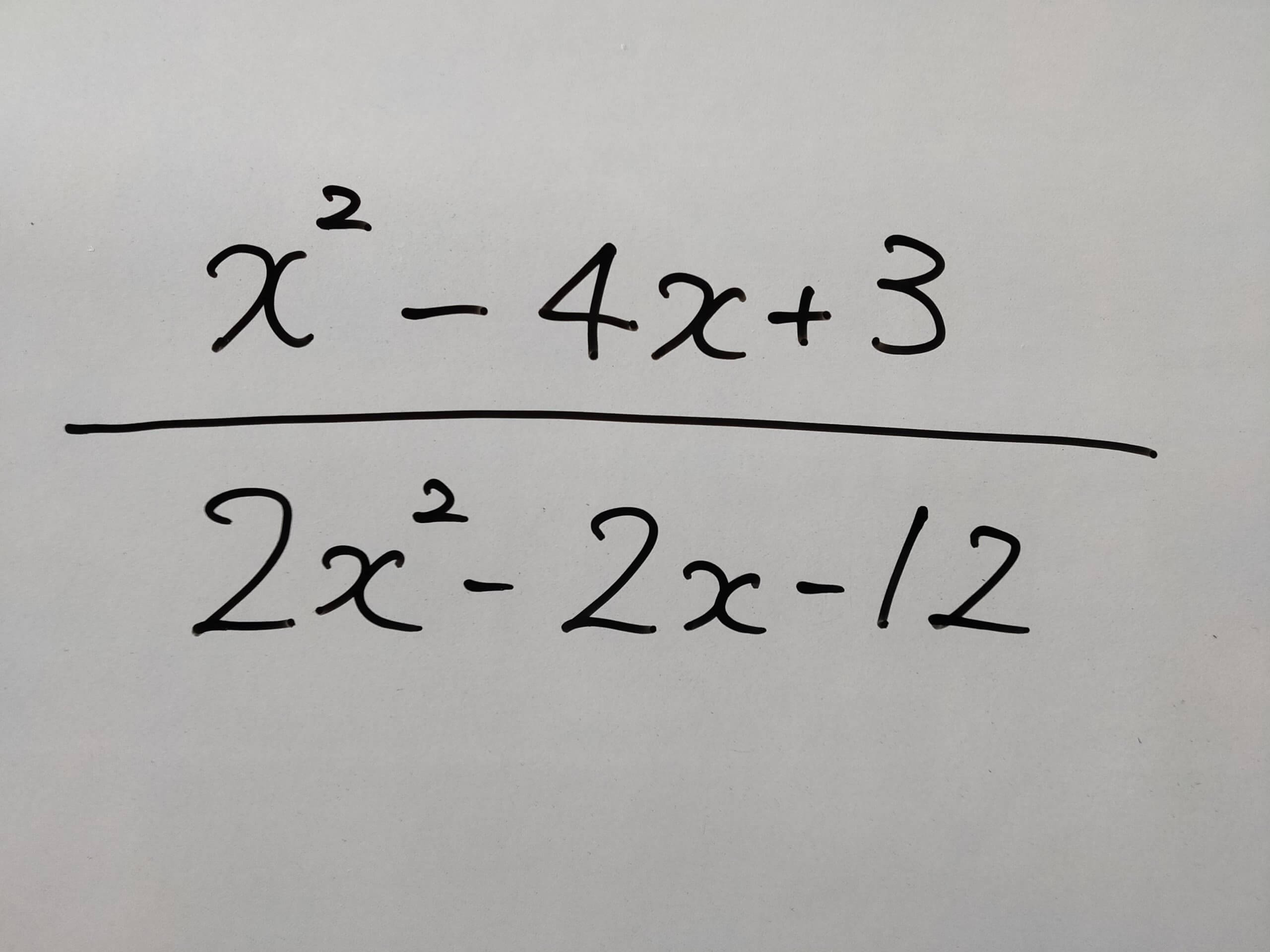分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	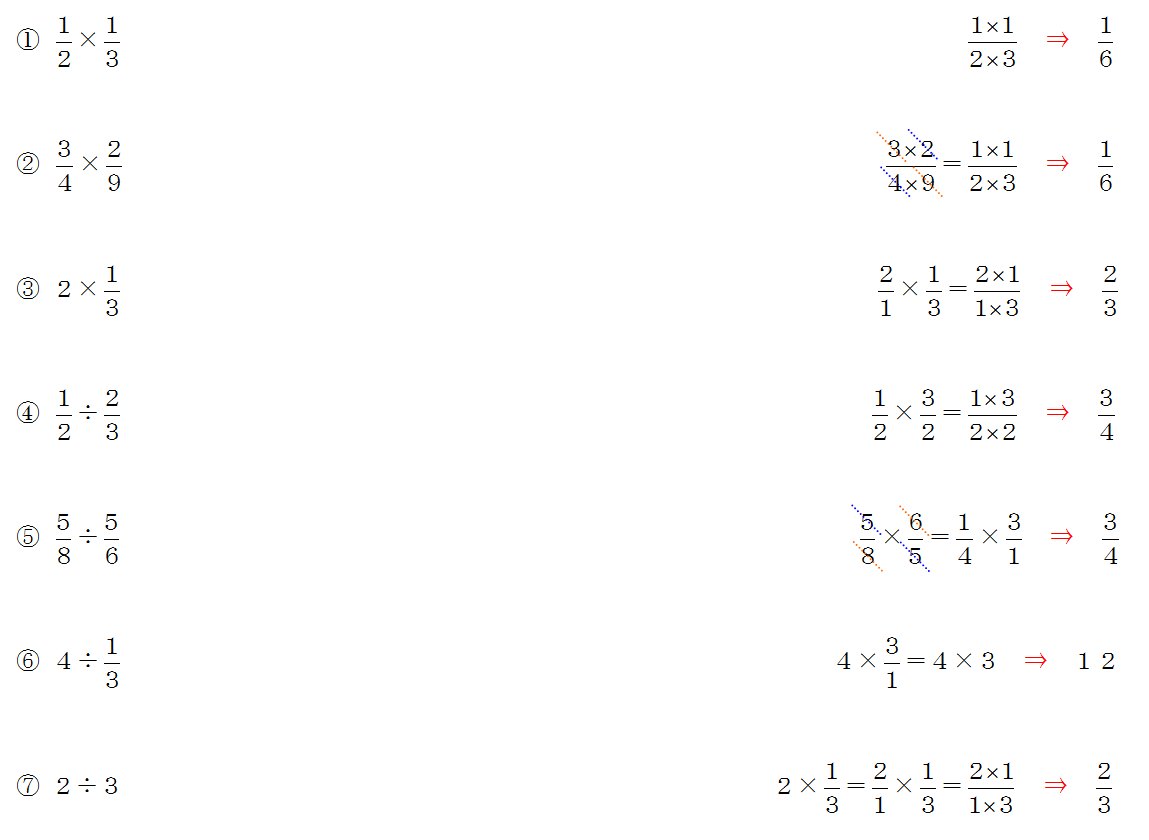分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	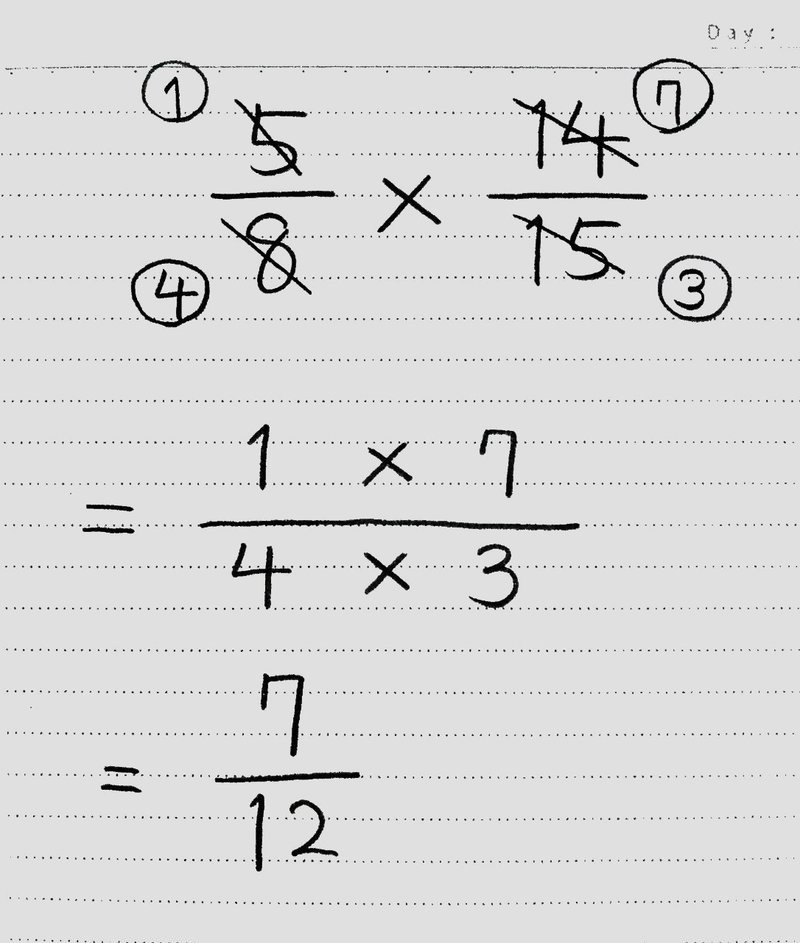分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	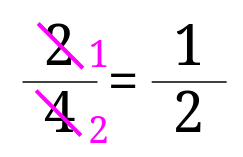分数足し算約分なし 問題 031 100	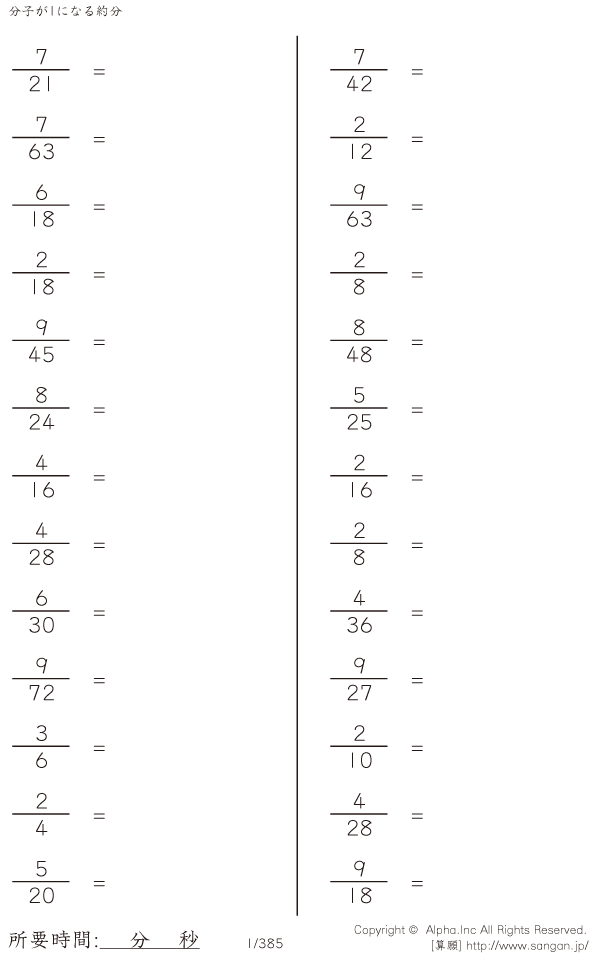分数足し算約分なし 問題 031 100
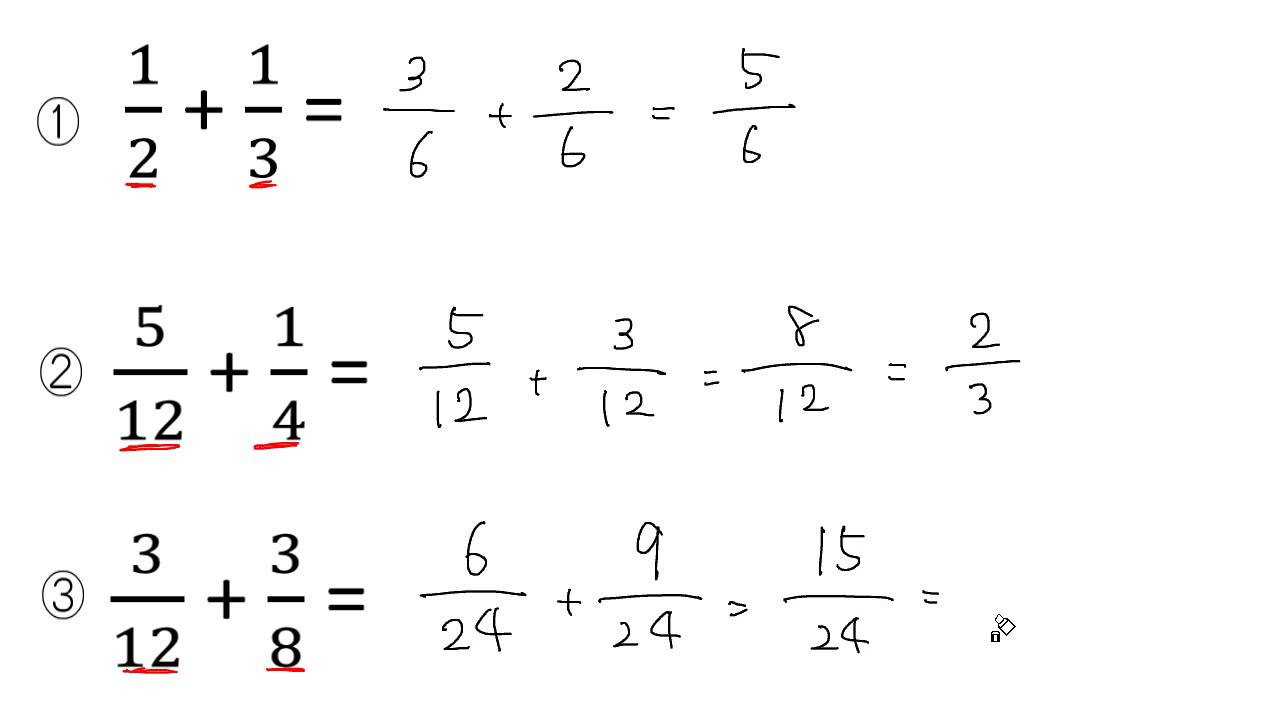分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	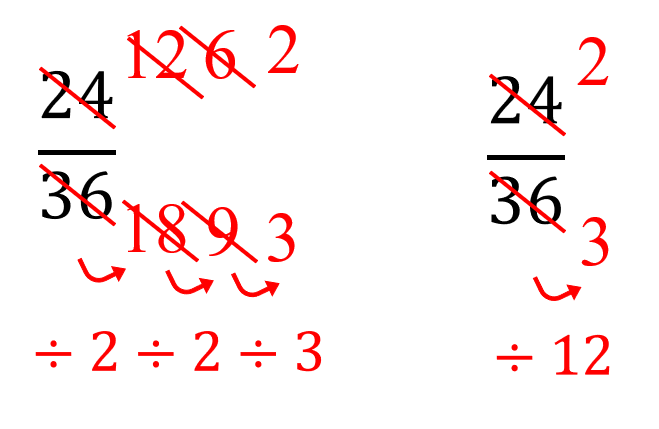分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	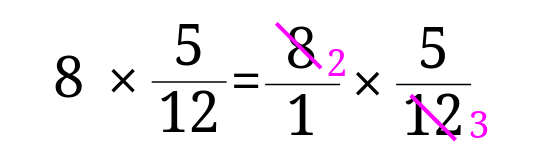分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
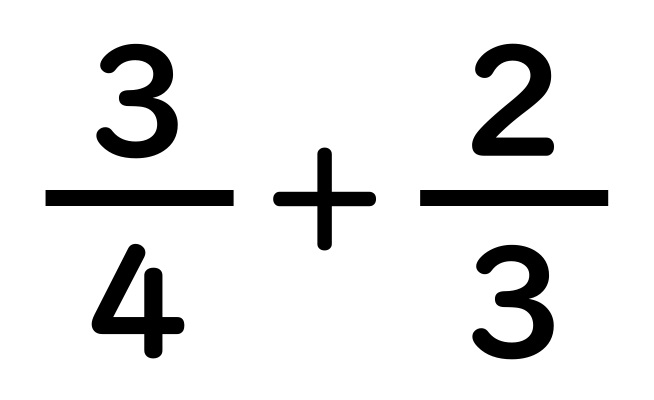分数足し算約分なし 問題 031 100	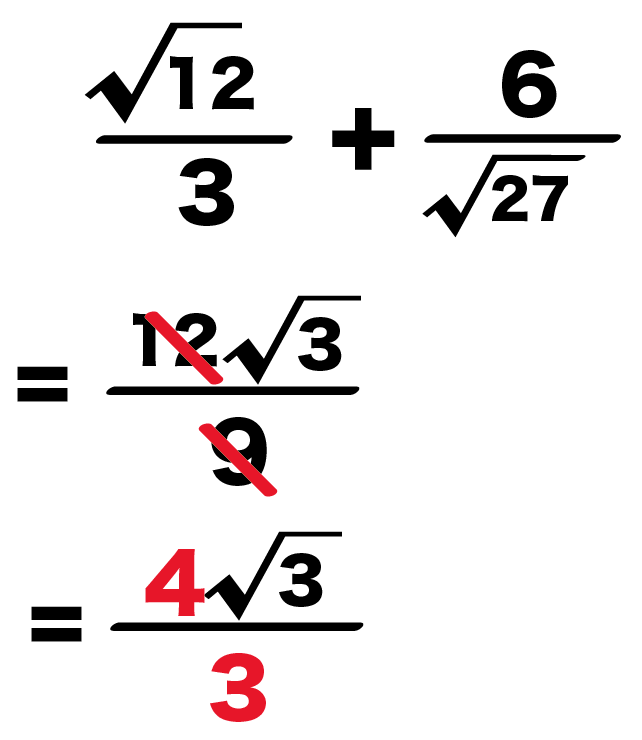分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100
分数足し算約分なし 問題 031 100	分数足し算約分なし 問題 031 100

分数の約分 a/bの分数の約分を最大公約数を求めることで計算しましょう。 a,bを最大公約数の値で割ればいいだけです。 最大公約数を求める記事を参考にしてください。 13/1は13と1最大公約数が13なので13/13=1 1/13=14となり 1/14となります。 #include 分数の足し算で「約分」が発生する条件 (2) 早速ですが、昨日の記事の続きです。 tsujimotterhatenablogcom 前回の記事では、分数の足し算の計算で約分が発生する条件について考えました。 特に、結果の分母・分子が素数 で約分されるならば、 が で

Incoming Term: 分数の約分, 分数の約分のコツ, 分数の約分問題, 分数の約分c言語, 分数の約分 プリント, 分数の約分の仕方, 分数の約分の仕方プリント, 分数の約分 java, 分数の約分 通分, 分数の約分 何年生,